Modèles macroéconomiques avec frictions financières et cycles d'assurance

Le phénomène des « cycles de souscription » est l'une des caractéristiques bien connues de certaines branches d'assurance et de réassurance. De tels cycles se composent d'une phase de tension au cours de laquelle les primes et les profits augmentent, alors que les capacités s'amenuisent, suivies de phases de relâchement pour lesquels les prix sont à la baisse et les capacités se reconstituent. De tels cycles se succèdent avec une certaine régularité dans le temps. Les phases de tensions peuvent apparaître très soudainement et sont parfois appelées « crises de passif », comme, par exemple, entre 1984 et 1986 lorsque, sur la plupart des marchés d'assurance, les primes ont presque triplé avant de diminuer lentement au cours de la décennie suivante.

De nombreux auteurs ont étudié ce phénomène. Ainsi, à l'aide de modèles autorégressifs d'ordre 2, les articles de Meier (2006) et Meier et Outreville (2006) tendent à confirmer l'existence de cycles de souscription en assurance de responsabilité pour la Suisse, les États-Unis, l'Allemagne de l'Ouest et la France sur une période de quarante ans (1957-1997).

D'un point de vue théorique, il est difficile d'expliquer de tels cycles. Si les marchés financiers sont parfaits, la prime d'assurance à l'équilibre concurrentiel est nécessairement égale à l'espérance corrigée du risque de la valeur actualisée des coûts des sinistres futurs. Cela résulte essentiellement de la condition d'absence d'opportunité d'arbitrage. Pour expliquer les cycles de souscription, il faut soit supposer que les sinistres sont cycliques (ce qui est réfuté empiriquement), soit faire intervenir des phénomènes complexes de retard dans les pratiques de déclaration et des décalages temporels d'ordre institutionnel. Dans l'approche classique, les cycles seraient ainsi des artefacts dus aux règles comptables, aux retards d'information et aux rigidités réglementaires (voir, par exemple, Cummins et Outreville (1987), Lamm-Tennant et Weiss (1997) ou Chen et al. (1999)).

Si l'on prend en compte les frictions sur les marchés de capitaux, des contraintes de capacité apparaissent. Les cycles de souscription proviennent alors de la dépendance de la capacité de l'industrie, à court terme, par rapport aux profits et aux pertes courantes. Selon cette approche, un cycle commence lorsque les capacités se trouvent réduites après des pertes exceptionnelles qui ont épuisé les réserves. Comme l'injection de nouveaux capitaux propres est coûteuse, les réserves se reconstituent prioritairement par le biais de la rétention des profits. Cette reconstitution progressive des réserves se traduit par une augmentation de la capacité et une intensification de la concurrence, qui favorise, en retour, la baisse des primes. Dans un tel contexte, les prix ne sont pas réellement périodiques, mais dépendent, à court terme, de la chronique des sinistres antérieurs.

Dans cet article, nous proposons un modèle macroéconomique dynamique dans lequel l'émission de nouvelles actions est coûteuse, du fait de frictions financières. Dans notre modèle, les assureurs déterminent leur offre de souscription proportionnellement à leur niveau de fonds propres comptables (leur capacité). Par agrégation, la capacité de l'industrie (fonds propres agrégés de l'industrie) est la variable d'état qui détermine la dynamique des rachats d'actions, des recapitalisations et des primes. Ainsi les compagnies d'assurance rachètent leurs actions (ou distribuent des dividendes exceptionnels), lorsque la capacité du secteur est élevée. Symétriquement, les émissions d'actions nouvelles ont lieu lorsque la capacité devient trop faible. La dynamique de la capacité est un processus réfléchi entre deux frontières. Il en résulte une oscillation des primes et de la capacité d'apparence quasi cyclique.

Une prédiction intéressante de notre modèle est que ces quasi-cycles doivent être asymétriques. Si l'on mesure la durée moyenne de la phase de relâchement (resp. de tension) par le délai moyen entre le niveau maximum (resp. minimum) et le niveau maximum (resp. minimum) des prix, notre analyse montre que la phase de marché de relâchement doit durer plus longtemps (en moyenne) que la phase de marché en tension, comme le suggère le graphique 1. De plus, cette différence s'avère d'autant plus grande que l'élasticité de la demande d'assurance est élevée.

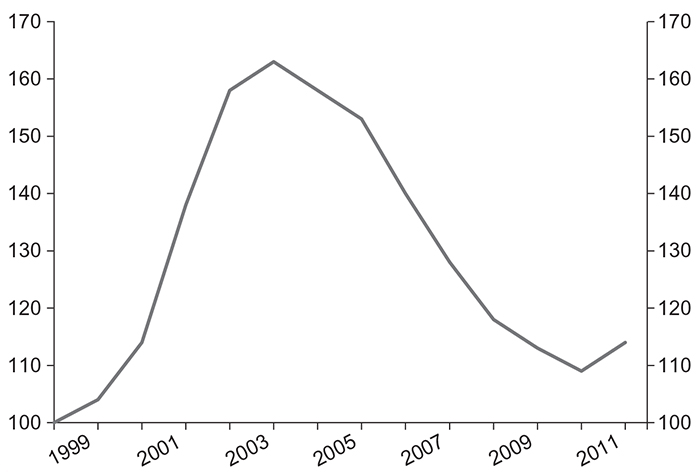
Note : ce graphique montre l'évolution de l'indice des prix de l'assurance (données du Conseil des agents et courtiers d'assurance aux États-Unis, CIAB 2013, base 100, 1999). La phase de relâchement dure plus longtemps que la phase de tension.

Source : The Council of Insurance Agents and Brokers, Market Surveys (https://www.ciab.com/business-intel/market-index-surveys/).

REVUE DE LA LITTÉRATURE

Notre article s'inscrit dans la lignée des travaux qui tentent de relier l'émergence des cycles aux variations de la valeur des sociétés d'assurance. Stewart (1984) et Bloom (1987) ont développé deux modèles simples en ce sens. Ils s'appuient sur une approche d'équilibre partiel où les déplacements des courbes d'offre d'assurance expliquent les cycles de souscription. La position de la courbe d'offre dépend de la valeur nette des compagnies et la forme des anticipations explique l'émergence et la durée des phases de prix élevé. Cagle et Harrington (1995) proposent un modèle d'offre d'assurance avec contraintes de capacité et un risque de défaut endogène. Si la demande est inélastique, le prix augmentera à la suite d'un choc négatif sur le capital. Choi et al. (2002) effectuent une comparaison empirique de six modèles alternatifs sur des données américaines entre 1935 et 1997. Ils montrent que le modèle de contrainte de capacité est cohérent avec les données, à long et à court terme. Gron (1994) donne des arguments empiriques qui tendent à confirmer les théories fondées sur les contraintes de capacité. L'article le plus proche du nôtre est celui de Winter (1994) : il développe un modèle en temps discret semblable au nôtre. Les assureurs accumulent des capitaux propres, afin d'éviter la faillite tout en satisfaisant la demande. Cette caractéristique implique une courbe d'offre à court terme croissante et dont la position est déterminée par le niveau de capital. De plus, le différentiel de coût entre le financement interne et l'appel aux fonds externes empêche le capital financier de s'adapter rapidement. Comme dans notre modèle, la variable d'état est la richesse nette totale des compagnies d'assurance et l'équilibre (avec anticipations rationnelles) se caractérise par la dynamique conjointe des prix de l'assurance et du ratio de la valeur de marché/valeur comptable (q de Tobin). Cependant, contrairement à notre modèle, la caractérisation récursive de la dynamique d'équilibre ne permet pas des solutions explicites.

Notre modèle peut être considéré comme une version en temps continu de Winter (1994). Nous obtenons des prédictions analogues à celles obtenues en temps discret avec l'avantage d'une caractérisation explicite de la dynamique d'équilibre. Cette caractérisation nous permet en particulier d'étudier précisément la dynamique des prix.

Le modèle

Notre modèle s'inscrit dans la lignée de la théorie de la ruine en temps continu (voir, par exemple, Gerber et Shiu 2004). Dans ce type d'approche, les contrats ont une durée de vie infinitésimale, ce qui permet de se concentrer sur les actifs et les passifs à court terme des assureurs. Les fonds propres comptables d'une compagnie (au passif) coïncident donc avec leurs réserves liquides (à l'actif).

Dans le modèle de ruine classique, la variation des réserves résulte de la différence entre primes perçues et sinistres réglés (augmentés des frais de gestion). Nous étendons ce modèle en laissant chaque compagnie décider de sa politique de souscription. Les primes d'assurance deviennent alors endogènes et résultent de l'équilibre entre offre et demande de contrats.

Dans le modèle classique, la compagnie choisit sa politique financière (émission ou rachat d'actions), de façon à maximiser sa valeur boursière en tenant compte du coût d'émission d'actions nouvelles, source de frictions financières.

Notre modèle généralise cette approche en introduisant la concurrence entre les compagnies. Nous supposons que les sinistres subis par chaque compagnie sont tous corrélés à un risque agrégé (du type catastrophe). Autrement dit, la diversification est incomplète et un risque commun subsiste.

Les primes d'assurance sont déterminées par l'équilibre entre l'offre et la demande de contrats. Nous caractérisons l'équilibre Markovien stationnaire dans lequel le prix de l'assurance est une fonction déterministe de la capitalisation boursière totale des compagnies. Formellement, un équilibre Markovien stationnaire est constitué d'un processus de capacité (réserves ou fonds propres comptables) et d'une fonction qui lie cette capacité au niveau des primes pour lesquels l'offre de contrats de chaque compagnie maximise sa valeur boursière et égale la demande de contrats à chaque instant.

À l'équilibre, la valeur boursière de chaque compagnie est égale à l'espérance corrigée du risque des dividendes futurs, nets des futures augmentations de capital. Un euro de financement interne a d'autant plus de valeur que les réserves sont faibles car, dans ce cas, la probabilité du recours futur à un financement externe, coûteux, est forte.

La capacité globale de l'industrie oscille entre deux valeurs extrêmes. Quand la valeur haute est atteinte (capacité maximum), la souscription de nouveaux contrats est peu profitable et les compagnies préfèrent réduire leur capacité en rachetant leurs actions. Quand la valeur basse est atteinte (capacité minimale), la souscription devient très rentable et les compagnies procèdent à une augmentation de capital.

Les primes d'équilibre sont donc fonction décroissante de la capacité totale. Lorsque les réserves sont reconstituées, la concurrence entre compagnies s'intensifie et la marge se réduit.

Il est intéressant d'étudier le processus des primes, qui oscille lui aussi entre deux valeurs extrêmes. En estimant la fonction de demande d'assurance, on peut mettre en évidence des propriétés testables des processus de prix et du book to value ratio des compagnies. Ainsi les primes ont une tendance de retour à la moyenne, qui dépend de l'ampleur des coûts de recapitalisation. Du fait des frictions financières, le taux de chargement reste toujours positif. Cette propriété, qui semble a priori surprenante dans un contexte de concurrence parfaite, n'est en fait pas contradictoire avec l'idée d'absence d'opportunité d'arbitrage. En effet, les investisseurs individuels ne peuvent pas vendre ou acheter directement des contrats d'assurance : ils doivent passer par l'intermédiaire d'une compagnie, c'est-à-dire vendre ou acheter des actions de ces compagnies. La concurrence implique que le ROE (return on equity) des compagnies est bien égal à l'espérance corrigée du risque des dividendes futurs et possède lui aussi une évolution oscillante conforme à l'expérience (cf. graphique 2 infra).

Notre modèle prédit que la dynamique des prix de l'assurance ne présente pas vraiment des cycles, mais plutôt des oscillations aléatoires entre deux valeurs. Lorsque les prix deviennent très élevés (parce que la capacité est faible), l'émission de titres (levée de fonds externes) devient profitable, cela augmente la capacité, ce qui intensifie la concurrence qui provoque un mouvement de prix à la baisse. Quand les prix deviennent très bas (car la capacité est élevée) et que l'activité d'assurance devient moins profitable, les entreprises préfèrent distribuer des dividendes exceptionnels, ce qui réduit la capacité et amorce la hausse du prix. Une simulation permet de mieux visualiser le phénomène (cf. graphique 3).

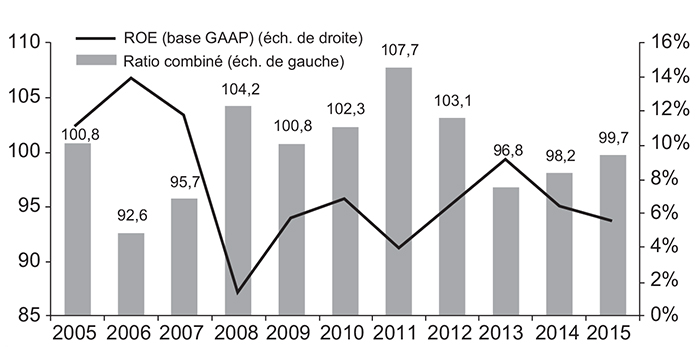
Source : Swiss Re Institute, Sigma Data.

Source : simulation des auteurs.

CONCLUSION

Notre modèle est une extension, en équilibre général, du modèle standard de la théorie de la ruine. Dans notre modèle, les compagnies ont un comportement concurrentiel d'offre face à un prix de marché qui dépend de la capacité totale de l'industrie. L'équilibre peut être calculé quasi explicitement. Les résultats obtenus sont conformes aux données empiriques. Les prix suivent une dynamique d'oscillation entre deux bornes avec des phases de remontées plus rapides que les phases de descente. Il ne s'agit pas à proprement parler de cycles, mais plutôt de mouvements aléatoires entre deux valeurs extrêmes. Les prix sont élevés lorsque les réserves sont faibles. Au contraire, lorsque le secteur a connu une phase propice à la reconstitution des réserves (peu de sinistres), la concurrence s'intensifie et les prix baissent. Ces résultats illustrent la puissance des nouveaux modèles macroéconomiques avec frictions financières. Ces modèles sont susceptibles de s'appliquer à d'autres questions concernant les effets macroéconomiques des politiques des compagnies d'assurance et de réassurance.